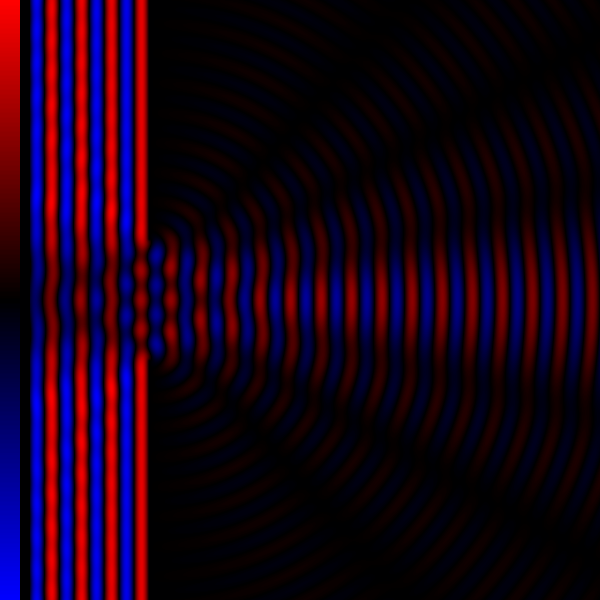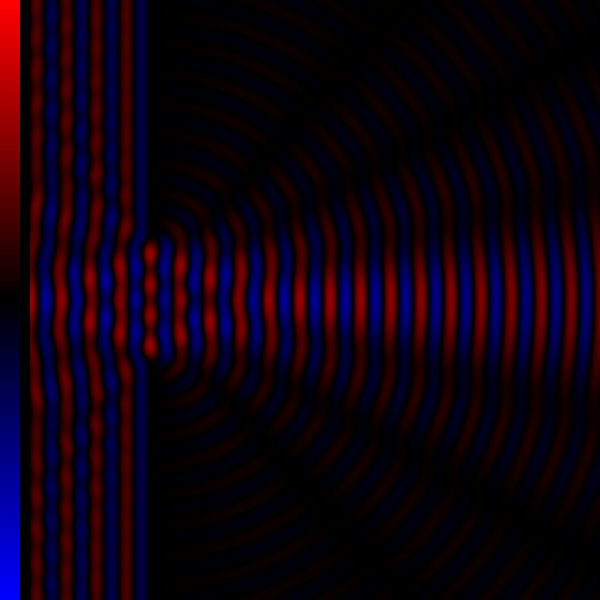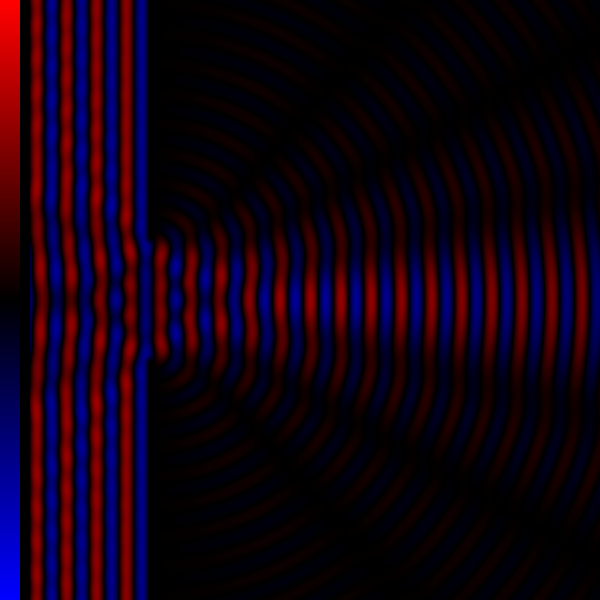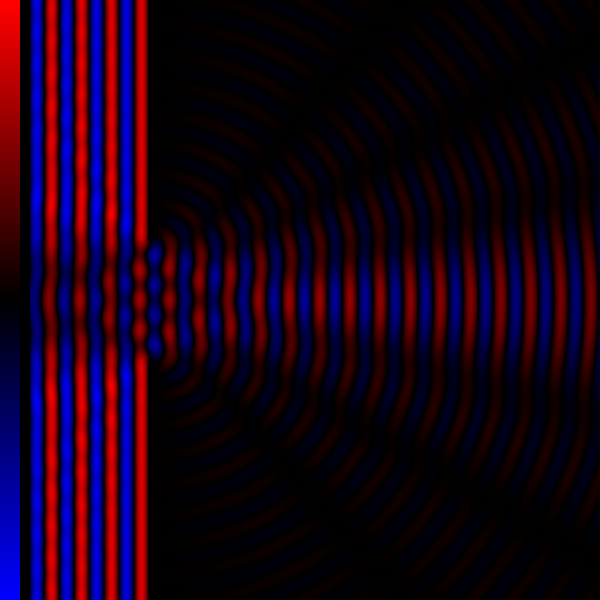
手机潜望长焦的衍射极限分辨率低于传感器分辨率
各个手机厂商的旗舰产品纷纷引入搭载高分辨率 CMOS 的潜望长焦,共同特点是不太大的光圈 & 较小的传感器尺寸——别忘了物理定律!
对于手机刷像素这件事还是直接玉音放送为好:
目前手机高像素都是0.8um的像素尺寸,但是即便是f1.2的衍射光斑都有1.2um。 现在手机还停留在f1.8上,更不必说现在手机镜头连像场中心都够不到衍射极限。 可能唯一有意义的使用方法是像素四合一或者视频单帧HDR。
以衍射极限能满足1080P分辨率(对于4:3比例就是1920*1440,2.76MP)来算的话,光圈最小要有等效F/52。这里已经考虑进了奈奎斯特采样定理。
我给你把等效F/52折算成另一套常见参数:1/4.4’的底,F/4.4的物理光圈
希望诸位能基此对手机的远射能力上限有直观的认识
“过个三四十年再看吧,没准光学和电子都能比十年前 135 好了 🐶”
现阶段的相机镜头,成像的原理均为小孔成像,“小孔”被称为光圈;小孔成像存在衍射极限。
圆孔衍射与艾里斑 (Airy Disk)
如果把细缝变成圆孔,就会形成圆孔衍射。
$R\gg a^{2}/\lambda$ 时,可观察到艾里斑 (Airy Disk),其强度分布为
$${\displaystyle I(\theta )=I_{0}\left[{\frac {2J_{1}(k\,a\sin \theta )}{k\,a\sin \theta }}\right]^{2}=I_{0}\left[{\frac {2J_{1}(x)}{x}}\right]^{2}}$$${\displaystyle I_{0}}$ 是艾里斑中心图案的最大强度, ${\displaystyle J_{1}}$ 是 1 阶第一类贝塞尔函数, ${\displaystyle k={2\pi }/{\lambda }}$ 是波数, ${\displaystyle a}$ 是光圈半径, ${\displaystyle \theta }$ 是观察角,即圆孔的轴线与孔中心和观察点之间的连线之间的角度, ${\displaystyle x=ka\sin \theta ={\frac {2\pi a}{\lambda }}{\frac {q}{R}}}$ ,其中 $q$ 是从观察点到光轴的径向距离, $R$ 是它到孔径的距离。
${\displaystyle J_{1}(x)}$ 的零点为 ${\displaystyle x=ka\sin \theta \approx 3.8317,7.0156,10.1735,13.3237,16.4706\dots}$ 由此可见,衍射图案中的第一个暗环出现在 ${\displaystyle ka\sin {\theta }=3.8317\dots}$ ,也可表达为
$${\displaystyle \sin \theta \approx {\frac {3.83}{ka}}={\frac {3.83\lambda }{2\pi a}}=1.22{\frac {\lambda }{2a}}=1.22{\frac {\lambda }{d}}}$$据此,可进一步计算出艾里斑的强度分布
当波长 $\lambda$ 一定时,孔径 $d$ 越小,艾里斑越明显
分辨率与瑞利判据 (Rayleigh Criterion)
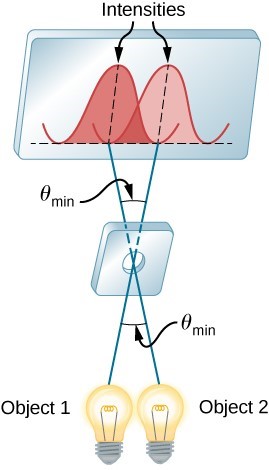
两个点光源在经过小孔成像后,会形成两个艾里斑;当两个点光源足够靠近时,艾里斑会重叠,导致难以分辨出这个像究竟是一个点光源还是两个点光源形成的。
数码相机使用离散的像素成像,因此要分辨出两个点光源,其像之间至少应间隔一个像素。
下图展示了受衍射影响,点光源在传感器上的成像情况。
为了区分明暗像素,引入瑞利判据 (Rayleigh Criterion)
两个相等强度的点光源,其中一个的中央极大值,刚好落在另一个的第一极小值,则称它们刚好能够分辨。
这个值被称为角分辨率 (Angular Resolution),当满足艾里斑形成的条件时,可通过下式计算
$${\displaystyle \theta \approx \sin \theta \approx 1.22{\frac {\lambda }{D}}}$$转为空间分辨率 $\Delta \ell$ ,其中 $f/\#$ 为镜头的光圈值
$${\displaystyle \Delta \ell \approx 1.22{\frac {f\lambda }{D}}=1.22\lambda \cdot (f/\#)}$$考虑奈奎斯特采样定理,单个像素的边长应为
$$s=\frac{\Delta \ell}{2}\approx 0.61\lambda \cdot (f/\#)$$手机长焦镜头的理论分辨率上限
$$像场对角线长度 = \frac {物理焦距}{全画幅等效焦距} \cdot \sqrt{{36^2 + 24^2}} \ mm$$2024-05-01 更新
考虑到长焦镜头普遍存在裁切 CMOS 的情况,像场对角线长度改为以 EXIF 记录的真实焦距与等效焦距之比计算
手机成像区域的常见长宽比为 4:3,根据勾股定理,不难推得下式
$$理论分辨率上限 = (\frac {像场对角线长度} {0.61\lambda \cdot (f/\#)})^2 × 0.48$$$$\text{CMOS 有效分辨率} = (\frac {像场对角线长度}{像素边长})^2 × 0.48 $$以 Galaxy S23 Ultra 的 10 倍变焦镜头为例,物理焦距 $27.20mm$,全画幅等效焦距 $230mm$,IMX754 像素边长为 $1.12 \mu m$, 光圈 $f/4.9$
$$像场对角线长度 = \frac {27.20mm}{230mm} \cdot \sqrt{{36^2 + 24^2}} \ mm = 5.12mm$$取红色光 $\lambda = 650 nm = 6.5×10^{-7} m$ ,求得
$$理论分辨率上限 = (\frac {5.12mm} {0.61 \cdot 650nm \cdot 4.9})^2 × 0.48 = \text{3.3 MP}$$然而
$$\text{CMOS 有效分辨率} = (\frac {5.12mm}{1.12 \mu m})^2 × 0.48 = \text{10 MP}$$这大概是为了更好地记录衍射现象吧(
取红色光 $\lambda = 650 nm = 6.5×10^{-7} m$,列举一些典型的手机长焦镜头的理论分辨率上限,苹果是最本分的 😇
| 型号 | 全画幅等效焦距/mm | 物理焦距/mm | CMOS | 像素边长/μm | 像场对角线长度/mm | CMOS 有效尺寸1 /Type-1 | 光圈/f | 理论分辨率上限/MP | CMOS 有效分辨率/MP | 理论上限/实际 |
|---|---|---|---|---|---|---|---|---|---|---|
| Galaxy Note20 Ultra | 123 | 14.20 | S5K3M5 | 1 | 5.00 | 3.60 | 3.0 | 8.5 | 12 | 71% |
| Galaxy S20 Ultra | 103 | 19.00 | IMX586 | 0.8 | 7.98 | 2.26 | 3.5 | 16 | 48 | 33% |
| Galaxy S21 Ultra | 240 | 30.60 | S5K3J1 | 1.22 | 5.52 | 3.26 | 4.9 | 3.9 | 10 | 39% |
| Galaxy S23 Ultra | 230 | 27.20 | IMX754 | 1.12 | 5.12 | 3.52 | 4.9 | 3.3 | 10 | 33% |
| Galaxy S24 Ultra | 115 | 18.60 | IMX854 | 0.7 | 7.00 | 2.57 | 3.4 | 13 | 48 | 27% |
| iPhone 15 Pro Max | 120 | 15.66 | IMX913 | 1.12 | 5.65 | 3.19 | 2.8 | 12 | 12 | 102% |
| OPPO Find X7 Ultra | 135 | 22.36 | IMX858 | 0.7 | 7.17 | 2.51 | 4.3 | 8.5 | 50 | 17% |
| Realme GT5 Pro | 65 | 15.38 | IMX890 | 1.00 | 10.2 | 1.56 | 2.6 | 47 | 50 | 94% |
| vivo X100 Pro | 100 | 16.57 | OV64B | 0.702 | 7.17 | 2.51 | 2.5 | 25 | 50 | 50% |
| vivo X100 Ultra | 85 | 22.48 | S5KHP9 | 0.56 | 11.44 | 1.40 | 2.67 | 56 | 200 | 28% |
| Xperia 1 VI | 85 | 10.30 | IMX650 | 1 | 5.24 | 3.43 | 2.3 | 16 | 13 | 120% |
| Xperia 1 VI | 170 | 19.01 | IMX650 | 1 | 4.84 | 3.72 | 3.5 | 5.8 | 11 | 52% |
| 华为 Mate 60 Pro | 95 | 14.60 | OV64B | 0.702 | 6.65 | 2.71 | 3.0 | 15 | 43 | 35% |
| 华为 P40 Pro+ | 269 | 28.21 | IMX520 | 1.22 | 4.54 | 3.97 | 4.4 | 3.2 | 6.6 | 49% |
| 华为 P60 Pro | 95 | 14.55 | OV64B | 0.702 | 6.63 | 2.72 | 2.1 | 30 | 43 | 71% |
| 荣耀 Magic6 Pro | 68 | 15.38 | S5KHP3 | 0.56 | 9.79 | 1.64 | 2.6 | 43 | 147 | 30% |
| 小米 14 Ultra | 120 | 19.40 | IMX858 | 0.7 | 6.99 | 2.57 | 2.5 | 24 | 48 | 50% |
| 一加 12 | 71.22 | 13.30 | OV64B | 0.702 | 8.09 | 1.98 | 2.6 | 30 | 64 | 46% |
请注意,这个计算结果是基于完美的光学模组得出的,现实中的光学模组远远达不到完美的程度,故实际的分辨率将低于理论上限。